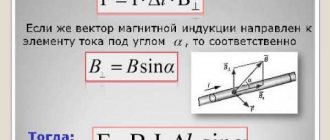
A conductor placed in a magnetic field through which an electric current is passed experiences the influence of Ampere force, and its value can be calculated using the following formula:
(1)
where and are the current strength and the length of the conductor, is the magnetic field induction, and is the angle between the directions of the current strength and magnetic induction. Why is this happening?
What is the Lorentz force - definition, when it occurs, obtaining the formula
It is known that electric current is the ordered movement of charged particles. It has also been established that while moving in a magnetic field, each of these particles is subject to the action of a force. For a force to occur, the particle must be in motion.
The Lorentz force is a force that acts on an electrically charged particle as it moves in a magnetic field. Its direction is orthogonal to the plane in which the vectors of particle velocity and magnetic field strength lie. The resultant of the Lorentz forces is the Ampere force. Knowing it, we can derive a formula for the Lorentz force.
The time required for a particle to pass a segment of a conductor, , where is the length of the segment and is the speed of the particle. The total charge transferred during this time through the cross section of the conductor is . Substituting here the time value from the previous equality, we have
(2)
At the same time, where is the number of particles located in the conductor under consideration. In this case, where is the charge of one particle. Substituting the value from (2) into the formula, you can get:
Thus,
Using (1), the previous expression can be written as
After reductions and translations, a formula appears for calculating the Lorentz force
Taking into account the fact that the formula is written for the force modulus, it must be written as follows:
(3)
Since , then to calculate the modulus of the Lorentz force, it does not matter where the velocity is directed - in the direction of the current or against it - and we can say that - this is the angle formed by the vectors of the particle velocity and magnetic induction.
Writing the formula in vector form will look like this:
is a vector product, the result of which is a vector with a modulus equal to .
Based on formula (3), we can conclude that the Lorentz force is maximum in the case of perpendicular directions of the electric current and magnetic field, that is, when , and disappears when they are parallel ().
It must be remembered that to obtain the correct quantitative answer - for example, when solving problems - you should use SI units, in which magnetic induction is measured in teslas (1 T = 1 kg s−2 A−1), force in newtons (1 N = 1 kg m/s2), current strength - in amperes, charge in coulombs (1 C = 1 A s), length - in meters, speed - in m/s.
Power units
Converting watts to amperes and vice versa is a relative concept, because these are different units of measurement. Amps are a physical quantity of electric current, that is, the speed at which electricity flows through a cable. Watt is the amount of electrical power, or the rate of electricity consumption. But such a translation is necessary in order to calculate whether the value of the current corresponds to the value of its power.
Relationship with other SI units
What amperes are from the point of view of the connection between electrical units can be seen in the following examples:
- at a current of 1 ampere (A), the cross-section of the conductor passes through itself a charge of 1 coulomb (C) in one second;
- when a charge of 1 ampere is applied to the plates of a capacitor with a capacity of 1 F, the voltage on the plates will increase, increasing by 1 V every second;
- the capacity of galvanic sources and batteries is measured in ampere-hours (A*h, or A*h), 1 A*h = 3660 C, this amount of electricity flows through the conductor in 1 hour;
- the maximum output power (watt) of rectifiers or power supplies is the second most important characteristic of such sources and is marked V*A;
- the amount of electricity in a lightning discharge is approximately 500 kiloamperes (1 kA = 10³ A);
- a 0.1 kilowatt (kW) incandescent light bulb consumes 0.5 A.
The designation of the number of amperes is applied to the housings of circuit breakers and fuses.
Converting amperes to watts and kilowatts
Knowing how to calculate the correspondence between amperes and watts is necessary in order to determine which device can withstand the power of connected consumers. Such devices include protective equipment or switching equipment.
Before choosing which circuit breaker or residual current device (RCD) to install, you need to calculate the power consumption of all connected devices (iron, lamps, washing machine, computer, etc.). Or, on the contrary, knowing the cost of a circuit breaker or protective shutdown device, determine which equipment will withstand the load and which will not.
To convert amperes to kilowatts and vice versa, there is a formula: I=P/U, where I are amperes, P are watts, U are volts. Volts are the mains voltage. In residential premises, a single-phase network is used - 220 V. In production, to connect industrial equipment, a three-phase electrical network is used, the value of which is 380 V. Based on this formula, knowing the amperes, you can calculate the correspondence to watts and vice versa - convert watts to amperes.
Situation: There is a circuit breaker. Technical parameters: rated current 25 A, 1-pole. You need to calculate what wattage of devices the machine can withstand.
The easiest way is to enter technical data into a calculator and calculate the power. You can also use the formula I=P/U, it will turn out: 25 A=x W/220 V.
x W=5500 W.
To convert watts to kilowatts, you need to know the following measures of power in watts:
- 1000 W = 1 kW,
- 1000 000 W = 1000 kW = MW,
- 1000,000,000 W = 1,000 MW = 1,000,000 kW, etc.
This means 5500 W = 5.5 kW. Answer: a machine with a rated current of 25 A can withstand the load of all devices with a total power of 5.5 kW, no more.
Apply a formula with voltage and current data in order to select the type of cable based on power and current. The table shows the current correspondence to the wire cross-section:
Copper cores of wires and cablesCode cross-section, mm²Copper cores of wires, cables
| Voltage 220 V | Voltage 380 V | |||
| Current, A | power, kWt | Current, A | power, kWt | |
| 1,5 | 19 | 4,1 | 16 | 10,5 |
| 2,5 | 27 | 5,9 | 25 | 16,5 |
| 4 | 38 | 8,3 | 30 | 19,8 |
| 6 | 46 | 10,1 | 40 | 26,4 |
| 10 | 70 | 15,4 | 50 | 33 |
| 16 | 85 | 18,7 | 75 | 49,5 |
| 25 | 115 | 25,3 | 90 | 59,4 |
| 35 | 135 | 29,7 | 115 | 75,9 |
| 50 | 175 | 38,5 | 145 | 95,7 |
| 70 | 215 | 47,3 | 180 | 118,8 |
| 95 | 260 | 57,2 | 220 | 145,2 |
| 120 | 300 | 66 | 260 | 171,6 |
How to convert watt to ampere
You need to convert watts to amperes in a situation where you need to install a protective device and you need to choose what rated current it should have. It is clear from the operating instructions how many watts a household appliance connected to a single-phase network consumes.
The task is to calculate how many amperes in watts or what kind of socket to connect to if the microwave oven consumes 1.5 kW. For ease of calculation, it is better to convert kilowatts into watts: 1.5 kW = 1500 W. We substitute the values into the formula and get: 1500 W / 220 V = 6.81 A. We round the values up and get 1500 W in terms of amperes - microwave current consumption is at least 7 A.
If you connect several devices simultaneously to one protection device, then in order to calculate how many amperes there are in watts, you need to add all the consumption values together. For example, the room uses lighting with 10 pcs LED lamps. 6 W, iron 2 kW and TV 30 W. First, all indicators need to be converted into watts, it turns out:
- lamps 6*10= 60 W,
- iron 2 kW=2000 W,
- TV 30 W.
60+2000+30=2090 W.
Now you can convert amperes to watts, to do this we substitute the values in the formula 2090/220 V = 9.5 A ~ 10 A. Answer: current consumption is about 10 A.
You need to know how to convert amps to watts without a calculator. The table shows the correspondence between the rate of electricity consumption and the current strength for single-phase and three-phase networks.
| Ampere (A) | Power, kWt) | |
| 220 V | 380 V | |
| 2 | 0,4 | 1,3 |
| 6 | 1,3 | 3,9 |
| 10 | 2,2 | 6,6 |
| 16 | 3,5 | 10,5 |
| 20 | 4,4 | 13,2 |
| 25 | 5,5 | 16,4 |
| 32 | 7,0 | 21,1 |
| 40 | 8,8 | 26,3 |
| 50 | 11,0 | 32,9 |
| 63 | 13,9 | 41,4 |
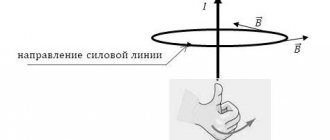
Determining the direction of the Lorentz force using the left-hand rule
Since in the world of macro objects the Lorentz force manifests itself as the Ampere force, you can use the left-hand rule to determine its direction.
You need to place your left hand so that the open palm is perpendicular and towards the lines of the magnetic field, four fingers should be extended in the direction of the current strength, then the Lorentz force will be directed where the thumb, which should be bent, points.
Types of electromagnetic forces
Definition 1
Electromagnetic forces are forces that act between bodies due to the fact that these bodies consist of charged moving particles between which magnetic and electric forces act.
Electromagnetic forces include:
- friction force $ \vec{ F_{tr}} $;
- elastic force $ \vec{ F_{control}} $;
- body weight $ \vec{ P} $.
Definition 2
The friction force $ \vec{ F_{tr}} $ is an electromagnetic force that arises due to the fact that the contacting bodies have uneven surfaces.
The friction force is always directed in the direction opposite to the movement. It has no application point. There are two types of friction force:
- Static friction force. It occurs when the bodies are at relative rest, in other words, when the bodies in contact are absolutely motionless relative to each other. The static friction force is always equal in magnitude to the external force and is directed in the opposite direction. It cannot exceed the maximum value $F_{tr.\max} = \mu N$.
- If the external force applied to the body becomes greater than $F_{tr.\max}$, then slipping occurs. The friction force in this case is called “sliding friction force”.
The sliding friction force is determined by the following formula:
$F_{tr.} = \mu N$, where
- $ \mu $ is the friction coefficient (dimensionless quantity), which depends only on the material of manufacture of the bodies and the degree of their processing;
- $N$ is the ground reaction force.
In addition to the above friction forces, one can also distinguish electromagnetic forces of viscous friction and rolling friction forces.
Definition 3
The elastic force $ \vec{ F_{exerc}} $ is an electromagnetic force that occurs during elastic deformation in a body.
It is directed opposite to the deformation. The modulus of elastic force can be calculated using the formula:
$ |F_{control}| = k \delta l$, where
- $k$ is the spring stiffness;
- $\delta l$ is the deformation.
Electromagnetic forces also include body weight.
Definition 4
The weight of a body $ \vec{ P} $ is the electromagnetic force with which a body acts on other bodies due to its attraction to the surface of the Earth.
If a body is at rest relative to the vertical or moves up or down uniformly, then its weight is equal to the force of gravity:
$P = mg$
If a body moves up with deceleration or down with acceleration, then its weight is significantly less than the force of gravity. You can find it using the following formula:
$P= m(ga)$
If a body falls freely, then a weightless state occurs. In this case, body weight is equal to zero:
$P = 0$
If a body goes down with deceleration or moves up with acceleration, then its weight exceeds the force of gravity. You can find body weight using the formula:
$P = m(g + a)$
In this case, the ratio of body weight to gravity can be called overload.
The formula for the weight of a body that moves uniformly accelerated through a vector difference can generally be expressed as follows:
$\vec{P} = m(\vec{g} -\vec{a})$
Motion of a charged particle in a magnetic field
In the simplest case, that is, when the magnetic induction and particle velocity vectors are orthogonal, the Lorentz force, being perpendicular to the velocity vector, can only change its direction. The magnitude of the speed, and therefore the energy, will remain unchanged. This means that the Lorentz force acts by analogy with the centripetal force in mechanics, and the particle moves in a circle.
In accordance with Newton's II law (), the radius of rotation of a particle can be determined:
.
It is necessary to note that with a change in the specific charge of the particle (), the radius also changes.
In this case, the period of rotation is T = = . It does not depend on speed, which means that the relative position of particles with different speeds will remain unchanged.
In a more complex case, when the angle between the particle velocity and the magnetic field strength is arbitrary, it will move along a helical trajectory - translationally due to the velocity component directed parallel to the field, and along a circle under the influence of its perpendicular component.
Practical use
The Ampere force is used in almost all electromechanical devices where it is necessary to cause the movement of real objects using electrical processes. One example application is measuring instruments.
The figure shows an example of a measuring device circuit. A power source (4) is connected to the axis. The axle is fixed in bearings (5), so it can rotate freely. There is a rectangular frame (1) on the axis through which current flows. It is located between the poles of a permanent magnet (2). The contacts are made in the form of spiral springs. An arrow (6) is attached to the axis, the tip of which moves along the measurement scale (7).
When current is passed through the conductor, a magnetic interaction appears and the frame begins to rotate. In this case, the pointer needle moves until the Ampere force balances the elastic force of both springs. The resulting indicator will characterize the current flowing through the conductor. The greater the current, the more the needle will deflect.
An industry such as electrical engineering is also based on Ampere's law. For example, electromagnetic induction is used in electric motors.
The motor converts electrical energy into shaft rotation. Current enters the frame through sliding brushes. It interacts with a permanent magnet, which leads to its rotation under the influence of the Ampere force. Modern engines can use several frames simultaneously. This allows you to increase the motor power and make the rotation of the axis smoother.
Engines operating on the basis of the effect under consideration are actively used in various types of electric transport - trams, trolleybuses, electric trains.
Another application of Ampere's law is in loudspeakers. There is a permanent magnet inside them. A change in current causes a change in the strength of the magnetic field, which leads to vibration of the membrane, producing sound of the desired frequency.
The attraction between conductors carrying current formed the basis for the precise definition of the unit of measurement 1 Ampere. In this case, an abstract situation was considered, which assumed the presence of two parallel conductors of infinite length. It was believed that each of them has an infinitesimal cross-section, the dimensions of which can be neglected.
It is accepted that throughout their entire length they are exactly one meter apart and in a vacuum. When a current of 1 Ampere passes, the force acting on each meter of conductors should be 0.0000002 Newton. This definition came into effect in 1948.
Application of Lorentz force in technology
Kinescope
The kinescope, which was installed until recently, when it was replaced by an LCD (flat) screen, in every TV, would not have been able to work without the Lorentz force. To form a television raster from a narrow stream of electrons on the television screen, deflection coils are used, in which a linearly varying magnetic field is created. Line coils move the electron beam from left to right and return it back; frame coils are responsible for vertical movement, moving the beam running horizontally from top to bottom. The same principle is used in oscilloscopes - devices used to study alternating electrical voltage.
Mass spectrograph
A mass spectrograph is a device that uses the dependence of the radius of rotation of a charged particle on its specific charge. The principle of its operation is as follows:
A source of charged particles that gain speed using an artificially created electric field is placed in a vacuum chamber in order to eliminate the influence of air molecules. The particles fly out from the source and, having passed along a circular arc, hit the photographic plate, leaving marks on it. Depending on the specific charge, the radius of the trajectory and, therefore, the point of impact changes. This radius is easy to measure, and knowing it, you can calculate the mass of the particle. Using a mass spectrograph, for example, the composition of lunar soil was studied.
Cyclotron
The independence of the period, and therefore the frequency of rotation of a charged particle from its speed in the presence of a magnetic field, is used in a device called a cyclotron and designed to accelerate particles to high speeds. A cyclotron is two hollow metal half-cylinders - dees (each of them resembles the Latin letter D in shape), placed with straight sides facing each other at a short distance.
The dees are placed in a constant uniform magnetic field, and an alternating electric field is created between them, the frequency of which is equal to the frequency of rotation of the particle, determined by the magnetic field strength and specific charge. Falling under the influence of an electric field twice during the rotation period (when moving from one dee to another), the particle accelerates each time, increasing the radius of the trajectory, and at a certain moment, having gained the required speed, flies out of the device through the hole. In this way, a proton can be accelerated to an energy of 20 MeV (megaelectronvolt).
Magnetron
A device called a magnetron, which is installed in every microwave oven, is another representative of devices that use the Lorentz force. The magnetron is used to create a powerful microwave field, which heats the internal volume of the oven where the food is placed. The magnets included in its composition correct the trajectory of electrons inside the device.
General understanding of the electromagnetic field
For a long time, ideas about the electric and magnetic fields were not connected with each other. Practical experiments confirmed that each of them has its own special properties. Research by Faraday and Maxwell showed that there is an electromagnetic field that can manifest itself as either electric or magnetic. It can be described with the power of a tension vector. If you know the magnitude and direction of a given vector, you can calculate the force of impact.
The first scientist to pay attention to the mutual influence of the magnetic field and current was the famous scientist H. K. Ørsted. He studied the effect of a conductor with current flowing through it on the position of the compass needle. After this, scientists began to systematically study various interaction options.
Ampere was born in 1775 in Lyon. Since childhood, he showed a passion for mathematics. As a teenager, he studied the works of Euler and Lagrange. Ampere became a professor of mathematics in 1809, and in 1814 he was elected to the Academy of Sciences. Although he primarily studied mathematics, he was interested in physics and some other sciences.
Ampere was not the first person to show interest in the connection between magnetic and electric fields, but he was the first to try to find an accurate mathematical description of the processes occurring. He not only established the fact of interaction between electric currents, but also formulated the law of this phenomenon.
Ampere proved that conductors begin to interact if a current flows through each of them. In this case, repulsive or attractive forces arise between them. In 1826, Ampere first published the results of his research, with the help of which he studied the interaction of parallel currents.
The figure below shows a diagram of one of Ampere's experiments, which measures the force acting on a current-carrying conductor in a magnetic field. The red arrow in the figure shows the direction of the current.
Based on experiments, the scientist made an assumption, which was later called the “Ampere hypothesis.” Understanding how current affects the magnetic field, he was able to prove that matter consists of a collection of extremely small circular currents. Each of them generates a very weak magnetic field. Since all these currents are randomly oriented, the magnetic field practically does not appear externally. However, in magnets all circular currents are equally directed and their effects add up. This explains their special properties and practical use.
Ampere, using his law, also explained the effect of magnetization. According to him, in some substances, under the influence of a magnetic field, circular currents are ordered, and they are gradually oriented in one direction.
This hypothesis became one of the sources of the theory of magnetism. She was able to explain the phenomenon only partially, since she did not answer the question of why some substances are only slightly affected by an external magnetic field. The question also remains unexplained: why, during magnetization, some substances create a magnetic flux co-directed with the external field (paramagnets), while others create a magnetic flux in the opposite direction (diamagnets).