Current is the movement of charged particles and is one of the key characteristics in an electrical circuit. This value is measured in Amperes. Electrical current measures the load on current-carrying wires, buses, and board traces.
Thanks to this value, you can understand how much energy flows in a conductor in a certain amount of time. The value can be calculated in different ways, depending on the data available.
Due to the fact that the solution options and known values may be different, you may encounter problems in the calculations. Next, let's look at how to correctly determine the current strength using different values.
Using power and voltage
If, of all the known data, you only have the value of power consumption and voltage, you need to use a simple formula that does not include resistance: P = IU
In this case, from the same formula you can get the following: I = P/U
This formula is suitable for a direct current circuit. And to calculate the current strength in circuits with alternating current (you may need this formula if you want to calculate the current strength in an electric motor), you also need to take into account the power factor (also called “cosine phi”).
In this case, for an electric motor with three phases, it is necessary to construct the calculation a little differently.
Find P, taking into account the efficiency: P1 = P2/η
In this formula, P 2 is the active shaft power and η is the efficiency. These values can usually be found on the engine itself.
After this, you need to find the total power taking into account the power factor (aka cos φ, its value is indicated on the engine): S = P1/cosφ
Next, determine the current consumption: Inom = S/(1.73 U)
1.73 is the root of three, this value is needed to calculate a three-phase circuit. The voltage value will depend on the method of switching on the electric motor (triangle or star) and Volts, most often 380.
Current calculation for a three-phase network
In the case of using a three-phase power supply, the current strength is calculated using the formula: I = P/1.73U, in which P means the power consumption, and U is the voltage in the three-phase network. 1.73 is a special coefficient used for three-phase networks.
Since the voltage in this case is 380 volts, the entire
formula will look like: I = P/657.4.
In the same way as in a single-phase network, the diameter and cross-section of conductors can be determined using a table showing the dependence of these parameters on various loads.
| Diameters of conductor cores (mm) | Conductor core cross-section (mm2) | Copper conductors | Aluminum conductors | ||
| Current (A) | Power, kWt) | Strength (A) | Power, kWt) | ||
| 0,8 | 0,5 | 6 | 2,25 | ||
| 0,98 | 0,75 | 10 | 3,8 | ||
| 1,13 | 1,0 | 14 | 5,3 | ||
| 1,38 | 1,5 | 15 | 5,7 | 10 | 3,8 |
| 1,6 | 2,0 | 19 | 7,2 | 14 | 5,3 |
| 1,78 | 2,5 | 21 | 7,9 | 16 | 6,0 |
| 2,26 | 4,0 | 27 | 10,0 | 21 | 7,9 |
| 2,76 | 6,0 | 34 | 12,0 | 26 | 9,8 |
| 3,57 | 10,0 | 50 | 19,0 | 38 | 14,0 |
| 4,51 | 16,0 | 80 | 30,0 | 55 | 20,0 |
| 5,64 | 25,0 | 100 | 38,0 | 65 | 24,0 |
In some cases, the calculation of current by voltage and power should be carried out taking into account the total reactive power present in electric motors, welding and other equipment. For such devices, the power factor will be 0.8.
By voltage or power and resistance
It also happens that to calculate the strength of the electric current, you need to use the voltage from a certain area or the magnitude of the load. Then the easiest way is to apply Ohm's law, which anyone who knows a little about physics knows.
If the voltage is unknown to you, but you know the value of power and resistance, carry out the calculation using the following formula: P=UI
Applying Ohm's law again, we get the following: U=IR
In this case: P=I2*R
We get the following formula: I2=P/R
In addition, you can apply the following calculation based on the same formulas and values: I=(P/R)1/2
Equipment / Power tools, electricians and online calculators / Online calculator - Ohm's law (current, voltage, resistance) + Power
The reason for writing this article was not the complexity of these formulas, but the fact that during the design and development of any circuits it is often necessary to go through a series of values in order to reach the required parameters or balance the circuit. This article and the calculator in it will simplify this selection and speed up the process of implementing your plans. Also at the end of the article I will give several methods for memorizing the basic formula of Ohm’s law. This information will be useful for beginners. Although the formula is simple, sometimes there is confusion about where and what parameter should be, especially at first.
In radio electronics and electrical engineering, Ohm's law and the formula for calculating power are used more often than any other formula. They determine the strict relationship between the four most common electrical quantities: current, voltage, resistance and power.
Ohm's law. This relationship was discovered and proven by Georg Simon Ohm in 1826. For a section of a circuit, it sounds like this: current is directly proportional to voltage, and inversely proportional to resistance
This is how the basic formula is written:
By transforming the basic formula, you can find two other quantities:
Power. Its definition is as follows: power is the product of the instantaneous values of voltage and current in any part of the electrical circuit.
Formula for instantaneous electrical power:
Below is an online calculator for calculating Ohm's law and Power. This calculator allows you to determine the relationship between four electrical quantities: current, voltage, resistance and power. To do this, just enter any two values. Using the up and down arrows you can change the entered value in steps of one. The dimension of the quantities can also be selected. Also, for the convenience of selecting parameters, the calculator allows you to record up to ten previously performed calculations with the dimensions with which the calculations themselves were performed.
When we studied at the radio engineering college, we had to memorize a lot of stuff. And to make it easier to remember, there are three cheat sheets for Ohm’s law. Here are the methods we used.
The first is a mnemonic rule. If we express resistance from the formula of Ohm's law, then R = glass.
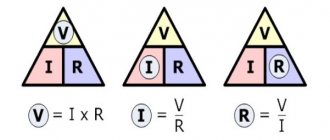
The second is the triangle method. It is also called the magic triangle of Ohm's law.
If we tear off the value that needs to be found, then in the remaining part we will get the formula for finding it.
Third. It is more of a cheat sheet that combines all the basic formulas for four electrical quantities.
It is as easy to use as a triangle. We select the parameter that we want to calculate, it is located in a small circle in the center and we get three formulas for its calculation. Next, select the one you need.
This circle, just like the triangle, can be called magical.
Using electromotive force, internal resistance and load
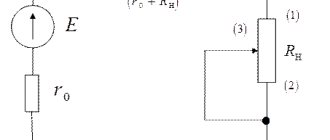
In some student textbooks there are so-called trick problems. These include those where there is an electromotive force and an internal resistance value.
Remembering Ohm's law, the strength of the electric current can be obtained as follows: I=E/(R+r)
Here E will be the electromotive force and r will be the internal resistance. R represents the load.
Selection of electrical appliances
To find out which household appliance is suitable for electrical wiring at home, and for which it is better to use an industrial one, you need to pay attention to its power. This parameter is always written in the operating manual or technical specifications of the device.
You should be wary if the power indicated is more than 1.5 kW, since for such devices you need to use an increased cross-section of the power supply wires. Typically, household electrical appliances have less power.
An exception may be washing machines, electric stoves, and some types of vacuum cleaners. Houses with electric stoves always have separate wiring for them, but to power the washing machine it is better to install a separate wire of increased cross-section.
Next, you should decide on the choice of circuit breaker for groups of electrical consumers. It should be selected specifically for a group, in order to save space in the distribution panel, and to be more free in connecting devices to different sockets. Which groups are better to choose :
- Electric stove;
- Washing machine and water heater;
- Other sockets and lighting.
In homes with electric stoves, the stove will have the highest consumption. Its power is estimated at 10 kW, which with a standard voltage of 220 V means a current consumption of 45 A, cosφ here is 1. The electric stove requires a separate machine, so here it is selected for 50 amperes.
The washing machine also has high current consumption. A standard washing machine consumes 2.5 kW, which corresponds to 12.5 A. Despite the cosφ = 0.8 of the washing machine’s electric motor, it contains a large number of electronics, so for the calculation we take cosφ = 1. The water heater has an even greater power - up to 8 kW . If you intend to use them simultaneously with the washing machine, it is worth taking a machine with a higher amperage, since the total power of these two devices will be 10.5 kW, that is, you need another 50 A machine. It would be better to make two separate machines: 40 A for the water heater, and 15 A - for a washing machine.
The remaining sockets and lighting can be assigned to a separate group. Their total energy consumption is estimated at 1.5 kW, that is, a 10 A machine will be enough for the third group.
Using the Joule-Lenz law
Some find it difficult to determine the current strength if there is:
- Time;
- Resistance value;
- The amount of heat generated from the conductor.
To solve the problem, you need to use the Joule-Lenz law: Q=I2Rt
Based on this formula, the calculation should be constructed as follows: I2=QRt
Or like this: I=(Q/Rt)1/2
Calculation of cosine phi (cos φ)
φ is the shift angle between the phase of current and voltage, and if the latter leads the current, the shift is considered positive, if it lags, it is negative.
cos φ is a dimensionless quantity that is equal to the ratio of active power to total power and shows how efficiently energy is used.
Formula for calculating cosine phi: cos φ = S / P
- S – total power, VA (Volt-ampere);
- P – active power, W.
Active power (P) is the real, useful, real power, this load absorbs all the energy and turns it into useful work, such as light from a light bulb. There is no phase shift.
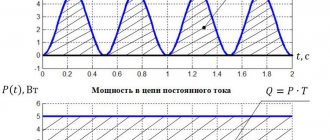
Formula for calculating active power: P (W) = I × U × cos φ
Reactive power (Q) is watt-free (useless) power, which is characterized by the fact that it does not participate in work, but is transmitted back to the source. The presence of a reactive component is considered a detrimental characteristic of a circuit, since the main purpose of the existing power supply is to reduce costs, and not to pump it back and forth. This effect is created by coils and capacitors.
Formula for calculating reactive power: P (VAR) = I × U × sin φ
The total power of an electrical appliance (S) is a total value that includes both active and reactive components of power.
Formula for calculating apparent power: S (VA) = I × U or S = √( P2 + Q2)